
Worksheet 2.3 Algebraic Fractions
Section 1 Factoring and Algebraic Fractions
As pointed out in worksheet 2.1, we can use factoring to simplify algebraic expressions, and in
particular we can use it to simplify algebraic fractions. Calculations using algebraic functions
are similar to calculations involving fractions. So when adding together fractions with different
denominators, we must first find the lowest common multiple.
Example 1 :
a + b
2
−
2a
5
=
5(a + b)
5 × 2
−
2(2a)
2 × 5
=
5a + 5b
10
−
4a
10
=
5a + 5b − 4a
10
=
a + 5b
10
Example 2 :
3
2x
−
y + 1
3xy
=
3y × 3
3y × 2x
−
2(y + 1)
2 × 3xy
=
9y
6xy
−
2y + 2
6xy
=
9y − (2y + 2)
6xy
=
9y − 2y − 2
6xy
=
7y − 2
6xy

Example 3 :
2
y + 1
+
3
y − 1
=
2(y − 1)
(y + 1)(y − 1)
−
3(y + 1)
(y − 1)(y + 1)
=
2y − 2
(y + 1)(y − 1)
−
3y + 3
(y − 1)(y + 1)
=
2y − 2 − 3y − 3
(y + 1)(y − 1)
=
−y − 5
(y + 1)(y − 1)
=
−(y + 5)
(y + 1)(y − 1)
Sometimes it is difficult to find a simple expression that is a multiple of two algebraic expres-
sions. When this is the case it is perfectly acceptable to multiply the two expressions together
even though this will not necessarily form the smallest common multiple. You should check
at the end of the calculation in the final fraction that there are no common factors in the
numerator and denominator; if there are, you can always cancel them to give an equivalent
but simpler fraction.
Exercises:
1. Simplify the following algebraic expressions:
(a)
x
3
+
x
2
(b)
m
7
−
m
5
(c)
4t
5
+
t
2
(d)
m+1
3
−
m−2
4
(e)
3m+4
7
+
m−1
2
(f)
y
y+1
−
y
y+3
(g)
5
t+1
+
4
t−3
(h)
3m
m+4
+
4m
m+5
(i)
4
y+1
−
5
y+2
(j)
7
4x
+
2
5xy
Section 2 Multiplication and Division
As in numerical fractions, the trick with simplifying the multiplication and division of algebraic
fractions is to look for common factors both before and after calculation. Once common factors
are cancelled out you get an equivalent fraction in its simplest form. Remember that dividing
Page 2
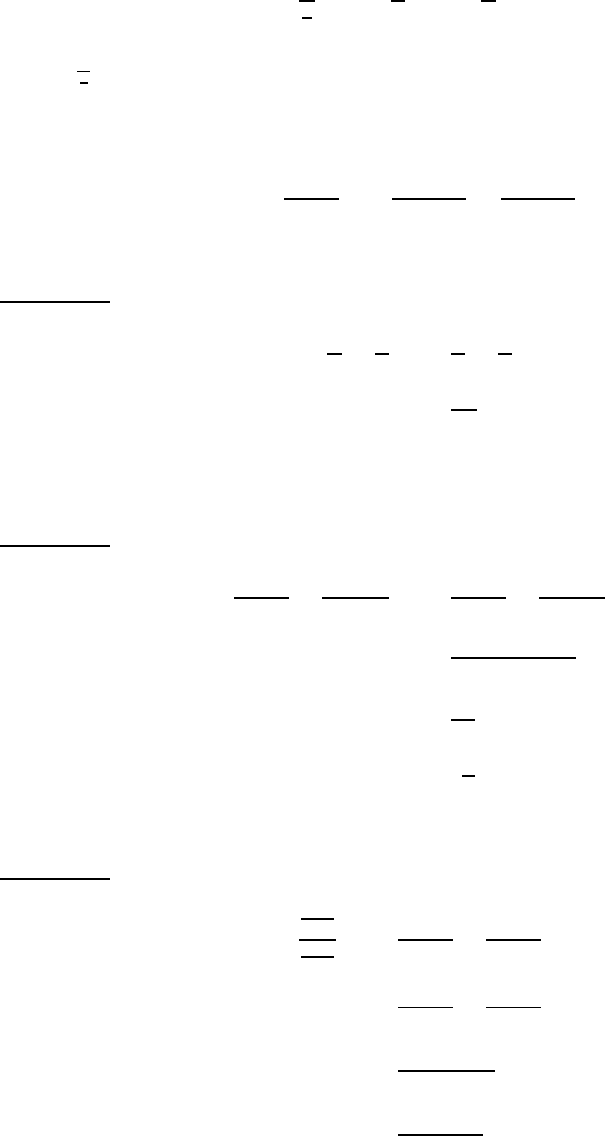
by a fraction is the same operation as multiplying by the reciprocal. That is
1
1
x
= 1 ÷
1
x
= 1 ×
x
1
= x
For example
1
1
6
means how many 6ths are in one whole? The answer is 6.
Also, an algebraic expression in the numerator or denominator should be treated as if it were
in brackets. For instance
−
x + 2
4
= −
(x + 2)
4
=
−x − 2
4
Example 1 :
x
2
÷
x
8
=
x
2
×
8
x
=
8x
2x
= 4
Example 2 :
8
x + 2
÷
7
2x + 4
=
8
x + 2
×
2x + 4
7
=
8 × 2(x + 2)
7(x + 2)
=
16
7
= 2
2
7
Example 3 :
x+1
4y
x+4
8y
=
x + 1
4y
÷
x + 4
8y
=
x + 1
4y
×
8y
x + 4
=
8y(x + 1)
4y(x + 4)
=
2(x + 1)
x + 4
Page 3

Example 4 :
4
xy
x+2
6
=
4
xy
×
6
x + 2
=
24
xy(x + 2)
Example 5 :
3
xy
×
y
6
=
6 3
x× 6 y
×
6 y
6 3 × 2
=
1
2x
Example 6 :
(
x
x−1
−
y
y−1
)
3
xy
=
(
(y−1)x
(y−1)(x−1)
−
(x−1)y
(x−1)(y−1)
)
3
xy
=
(
xy−x−xy+y
(x−1)(y−1)
)
3
xy
=
−x + y
(x − 1)(y − 1)
×
xy
3
=
(y − x)xy
3(x − 1)(y − 1)
Exercises:
1. Simplify the following algebraic expressions:
(a)
m
16
÷
5m
12
(b)
3m
8
÷
15m
20
(c)
6x+3
8
÷
2x+1
12
(d)
9xy
7
÷
6x
3
(e)
6pq
5
÷
12p
7
(f)
3(x+1)
8
÷
5(x+1)
16
(g)
4x
7
6xy
5
(h)
m+1
2
−
m−1
3
m+1
5
(i)
3
pq
×
4p
p+1
(j)
8(x+3)
9
×
12(x+1)
4(x+3)
Page 4

Section 3 Solving Equations
Sometimes we are asked to solve an equation for a particular variable. This means that
only the variable should be on one side of an equality sign and the other information in the
equation should be on the other side. This is similar to solving equations in one variable as in
Worksheet 2.2. However, you may end up with an algebraic expression on one side involving
other variables rather than just a number. You should attack these questions in the same way
as solving equations for one variable.
The following examples and exercises use some of the techniques given in sections one and two
of this worksheet.
Example 1 :
x − 2
3
+
x + 1
5
= 3
Multiply each side by 15 - this will eliminate the fractions:
15 × (
x − 2
3
+
x + 1
5
) = 15 × 3
15
x − 2
3
+ 15
x + 1
3
= 45
5(x − 2) + 3(x + 1) = 45
5x − 10 + 3x + 3 = 45
8x − 7 = 45
8x = 52
x =
52
8
=
13
2
Page 5
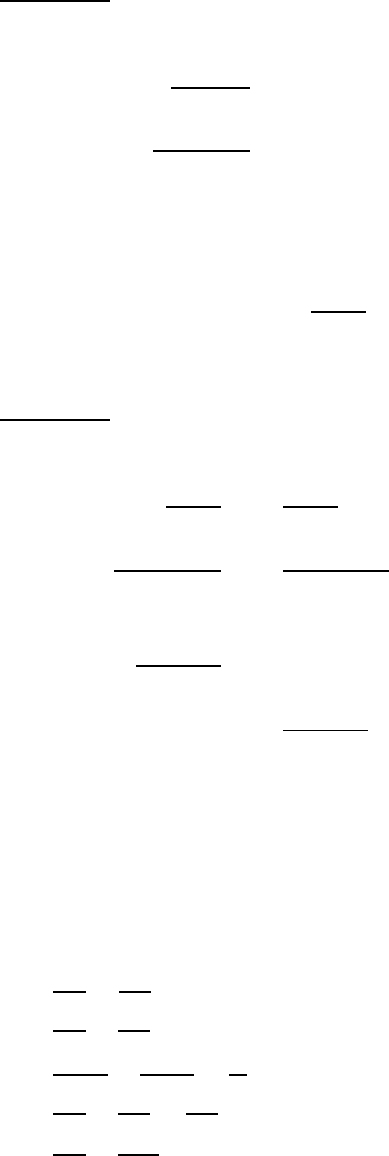
Example 2 :
Solve for x in terms of y.
1 + 2xy
y + 1
= 3x
(y + 1) ×
(1 + 2xy)
(y + 1)
= (y + 1)3x (multiplying both sides by (y + 1))
1 + 2xy = 3xy + 3x
1 = xy + 3x
1 = x(y + 3) (factoring to separate the x)
x =
1
y + 3
Example 3
:
Solve for y in terms of x.
4 + x
3y
2
=
x + 1
2y
6y
2
(4 + x)
3y
2
=
6y
2
(x + 1)
2y
(multiply both sides by 6y
2
)
2(4 + x) = 3y(x + 1)
2(4 + x)
(x + 1)
= 3y isolate y
y =
2(4 + x)
3(x + 1)
In the last two steps, we were aiming to make x the subject of the equation.
Exercises:
1. Solve for x:
(a)
x+8
5
−
x−2
3
= 4
(b)
x+1
3
+
x−4
2
= 5
(c)
3(x−2)
4
−
2(x+1)
5
=
1
10
(d)
4
x+1
+
3
x−4
=
2
x+1
(e)
5
x+3
+
2
2x+6
= 4
Page 6

2. Solve for x in terms of y:
(a) 3xy = 8
(b)
4
x+1
=
3
y+2
(c) 4(y + 1) − 3(x + 5) = 8
(d)
1+y
2+x
= 3y
(e) 5xy + 3xy
2
= 7
Page 7

Exercises 2.3 Algebraic Fractions
1. Simplify the following:
(a)
x
3
+
x
4
(b)
2
2xy
+
4
xy
3
(c)
3x+1
2
− (6x + 5)
(d)
3
b−1
−
4
b−2
(e)
2x+2
y
x+1
xy
(f)
2
x
2
−4x
+
4
x−4
(g)
1
x+1
2−1
(h)
1
x+1
−
1
x+2
+
1
x+3
(i)
4a
7
+
3a+5
2
−
3(a+2)
4
(j)
3p
12
− (
p
2
−
p
4
+
5p
6
)
2. Simplify the follwing:
(a)
4(x+1)
3
−
5(x−2)
2
(b)
x
2
+3x
x+4
×
2x+8
5x
(c)
8x−24
4
÷
x+7
12
(d)
y
2
−6y
y+5
×
3y+15
2y−12
(e)
5m−7
4m+8
÷
m+2
3m+6
(f)
6p−3
4
÷
−4p+2
12
Page 8

Answers 2.3
Section 1
1. (a)
5x
6
(b)
−2m
35
(c)
13t
10
(d)
m+10
12
(e)
13m+1
14
(f)
2y
(y+1)(y+3)
(g)
9t−11
(t+1)(t−3)
(h)
m(7m+31)
(m+4)(m+5)
(i)
−y+3)
(y+1)(y+2)
(j)
35y+8
20xy
Section 2
1. (a)
3
20
(b)
1
2
(c) 4
1
2
(d)
9y
14
(e)
7q
10
(f) 1
1
5
(g)
10
21y
(h)
5(m+5)
6(m+1)
(i)
12
q(p+1)
(j)
8(x+1)
3
Section 3
1. (a) x = −13 (b) x = 8 (c) x = 5
5
7
(d) x = 1 (e) x = −1
1
2
2. (a) x =
8
3y
(b) x =
4y+5
3
(c) x =
4y−19
3
(d) x =
1−5y
3y
(e) x =
7
y(5+3y)
Exercises 2.3
1. (a)
7x
12
(b)
y
2
+4
xy
3
(c)
−9(x+1)
2
(d)
−(b+2)
(b−1)(b−2)
(e) 2x
(f)
2(1+2x)
x(x−4)
(g)
1
x+1
(h)
x
2
+4x+5
(x+1)(x+2)(x+3)
(i)
37a+28
28
(j)
−5p
6
2. (a)
−7x+38
6
(b)
2(x+3)
5
(c)
24(x−3)
x+7
(d)
3y
2
(e)
3(5m−7)
4(m+2)
(f) −
9
2
Page 9
